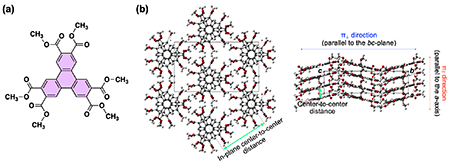
The acquisition and understanding of electrical conducting nature in organic materials, which are essentially insulators, has led to the development of organic electronics, bringing new material tools to conventional electronic devices developed with silicon technology. This is true for the thermal transport properties of organic materials, which is expected to become promising materials for new thermal management technologies if we understand essence of thermal conductivity through molecules, which has been conventionally thought to be low. However, due to the complex components of organic materials, such as wide variety of molecules, intermolecular forces, assembly structures, and morphologies, their thermal transport properties have not been comprehensively studied and remains poorly understood. To address this issue, we focused on organic single crystals, in which the position and orientation of molecules are determinable and intramolecular chemical bonds and intermolecular forces are clearly defined. In this study, we investigated the relationship between π-π interactions and thermal transport properties using an organic single crystal to clarify the role of intermolecular forces in thermal transport ^[1]. Although π-stacking is a structural motif ubiquitously observed in aromatic compound assemblies and is well known to provide charge and exciton transport pathways, its contribution to thermal transport remains unclear. The target material was a single crystal of triphenylene-2,3,6,7,10,11-hexacarboxylic acid methyl ester (TP), which has a highly ordered 1D π-stacked column structure ^[2] (Fig. 1a, b).

Fig. 1.	(a) Schematic structure of TP. (b) Single-crystal X-ray structure of TP, showing the intra- and intercolumnar center-to-center distances between π-stacked TP molecules.

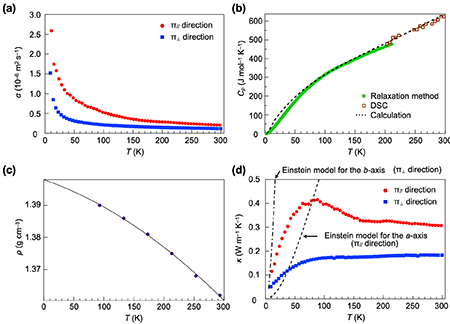
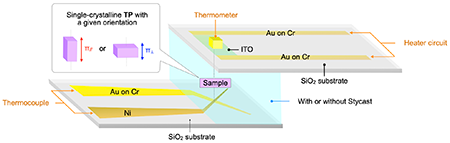
　To discuss the anisotropy and temperature dependence of thermal conductivity (κ), thermal diffusivity (α), specific heat at constant pressure (C_p), and density (ρ) were evaluated in the temperature range below room temperature by micro thermal wave analysis (μTWA), relaxation method by Physical Property Measurement System (PPMS) and differential scanning calorimetry (DSC), and single crystal X-ray structure analysis, respectively, and the thermal conductivity was obtained at each temperature using the equation κ = αC_pρ. In the μTWA method, temperature waves are generated in the crystal by Joule heating with an AC voltage applied to indium tin oxide (ITO) film that are contacted with the crystal. The temperature waves that pass through the crystal is detected with a sensor (Au-Ni thermocouple) installed on the opposite side of the crystal, and converting the voltage. Then, thermal diffusivity can be evaluated from the phase difference between input and output signals (Fig. 2). Anisotropic thermal diffusivity can be obtained using the μTWA method even in a micro-order sized single crystal by changing the orientation of the single crystal in accordance with the direction in which the temperature wave is input.

Fig. 2.	(a) Schematic illustration of the experimental setup for μTWA measurements.

Fig. 3.

(a) Temperature dependence of the thermal diffusivity parallel (α//) and perpendicular (α⊥) to the π-stacked columns of TP. (b) Temperature dependence of the specific heat (Cp) of TP measured using the relaxation method (green filled circles) and DSC (brown open squares), along with those calculated using the Einstein and Debye specific heat models (black broken curve). (c) Temperature dependence of the density of TP and its extrapolation curve. (d) Temperature dependence of thermal conductivity in the directions parallel (κ//) and perpendicular (κ⊥) to the π-stacked columns of TP, along with those calculated using the Einstein thermal conductivity model for a- and b-axes.

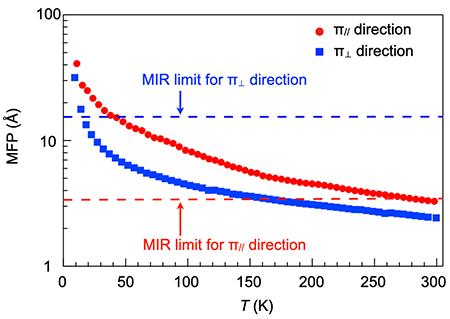
　The temperature dependence of α, C_p, ρ, and κ calculated from κ = αC_pρ for a TP single crystal are shown in Fig. 3a-d. The thermal conductivity (κ_//) in the direction parallel to the π-stacking (π_//) at room temperature is less than twice that (κ_⊥) in the direction perpendicular to the π-stacking (π_⊥). However, their temperature dependence is quite different. κ_// exhibits crystalline thermal conduction behavior, whereas κ_⊥ exhibits amorphous thermal conduction behavior even though it is a single crystal (Fig. 3d). In the π_// direction, the temperature dependence of the thermal diffusivity (α_//) shows approximately α_// ∝ T^-1, suggesting phonon-phonon scattering occurs. Phonons are quantized lattice vibrations, and it is known that vibrational modes, called acoustic phonons, are the principal carriers of thermal conduction. Using the temperature dependence of thermal diffusivity and the sound velocity (corresponding to longitudinal acoustic phonon group velocity) determined from ultrasonic measurements, we obtained the MFP, which is longer than the Mott-Ioffe-Regel (MIR) limit in almost all the temperature range below the room temperature, concluding that acoustic phonons carry thermal energy in the π_// direction (Fig. 4). The MIR limit is the criterion for the picture of coherent phonon to be valid, and when the carrier has an MFP longer than this criterion, the picture of coherent phonon keeps valid. In contrast, the thermal diffusivity in the π_⊥ direction (α_⊥) shows the temperature dependence of α_⊥ ∝ T^-0.41〜T^-0.54, and furthermore gives an MFP shorter than the MIR limit in almost all the temperature range below the room temperature (Fig. 4), indicating that the contribution of acoustic phonons to thermal in the π_⊥ direction is unobservably small in the π_⊥ direction.

　Since organic materials have intramolecular degrees of freedom, thermal energy should be stored in intramolecular vibrations. In fact, the temperature dependence of the specific heat of a TP single crystal indicates that thermal energy is stored in intramolecular vibrations. However, since intramolecular vibration is a highly localized vibrational mode, the question arises regarding how this thermal energy is transported in a crystal. We compared our experimental results with the Einstein thermal conduction model, which can describe the propagation of localized vibrations, and revealed that the propagation of thermal energy stored in intramolecular vibrations does not obey the Einstein thermal conduction model (Fig. 3d). In other words, intramolecular vibration itself is not considered to be a thermal carrier. Given that only thermal conduction by acoustic phonons is observed in the π_// direction, it is thought that thermal energy stored in intramolecular vibrations transfers to acoustic phonons by the coupling between them, and then the thermal energy is carried by acoustic phonons. In this case, intramolecular vibrational modes with energies above the Debye temperature, such as those excited around the room temperature, are less likely to couple with acoustic phonons with energies below the Debye temperature, resulting in less efficient thermal-energy transfer between them and consequently shorter mean free paths. This is considered to be the reason why, in general, the thermal diffusivity of organic materials, not only TP, is as small as 10^-7 m²·s^-1 around the room temperature. Since acoustic phonon thermal conduction has not been observed in the π_⊥ direction, the thermal energy stored in the intramolecular vibrations is transported in a form other than acoustic phonons. However, the transport mechanisms are not yet found, which will be addressed in the future.

Fig. 4.	Temperature dependence of mean free paths and MIR limits in the π// and π⊥ directions.

　The above results indicate that acoustic phonons are formed in the π-stacked columnar structure, and are responsible for thermal conduction, but that the contribution of acoustic phonons to thermal conduction in the π_⊥ direction, where only non-directional van der Waals forces work, is small. The results also suggest that thermal energy stored in localized intramolecular vibrations is also transported by acoustic phonons. We are currently investigating the relationship between various intermolecular forces including hydrogen bonding and thermal transport properties using other organic single crystals, and it is expected that these studies will further deepen understanding of thermal transport in organic materials.